Topic 16 Financial Fraud Analytics

16.1 Introduction to Financial Fraud

  • Financial institutions deliver several kinds of critical services usually managing high-volume transactions.

  • Each of these services is afflicted by specific frauds aiming at making illegal profits by unauthorized access to someone’s funds

  • Earnings manipulation and accounting fraud leads to reduced firm valuation in the long run and a public distrust in the company and its management.

  • The phenomena of earnings manipulation is not new globally. In 2001, Enron filed for bankruptcy after an accounting fraud resulted in $ 74 billion loss to the shareholders

  • Firms can manipulate earnings by utilizing their accounting choices known as accrual manipulations.

16.1.1 Types of Financial Fraud

There are various types of financial fraud. The following lists types of financial frauds as listed in Al-Hashedi & Magalingam (2021)

  • Credit Card Fraud
  • Mortgage Fraud
  • Money Laundering
  • Financial statement fraud
  • Securities and commodities fraud
  • Insurance Fraud
  • Cryptocurrency Fraud
  • Cyber Financial Fraud

16.1.2 ML and AI for Fraud Detection

There are various statistics and ML based classification techniques which are used for detecting fraud. Some of these techniques are

  • Support Vector Machines
  • Naive Bayes
  • Neural Network and Deep Learning
  • Random Forests
  • Logistic Regression
  • KNN
  • Decision Trees
  • Genetic Algorithms
  • Clustering

Ali et al. (2022), Bin Sulaiman, Schetinin, & Sant (2022), Ashtiani & Raahemi (2021), Al-Hashedi & Magalingam (2021), Sadgali, Sael, & Benabbou (2019) provide a review of ML and AI techniques used for financial fraud detection. Bin Sulaiman et al. (2022) provides a review of ML approaches used for Credit Card Fraud Detection.

16.1.3 ML and AI based Fraud Detection System for Credit Card Fraud

Fig-16.1 providesan example of a credit card fraud detection system (source: Le Borgne, Siblini, Lebichot, & Bontempi (2022) Link)

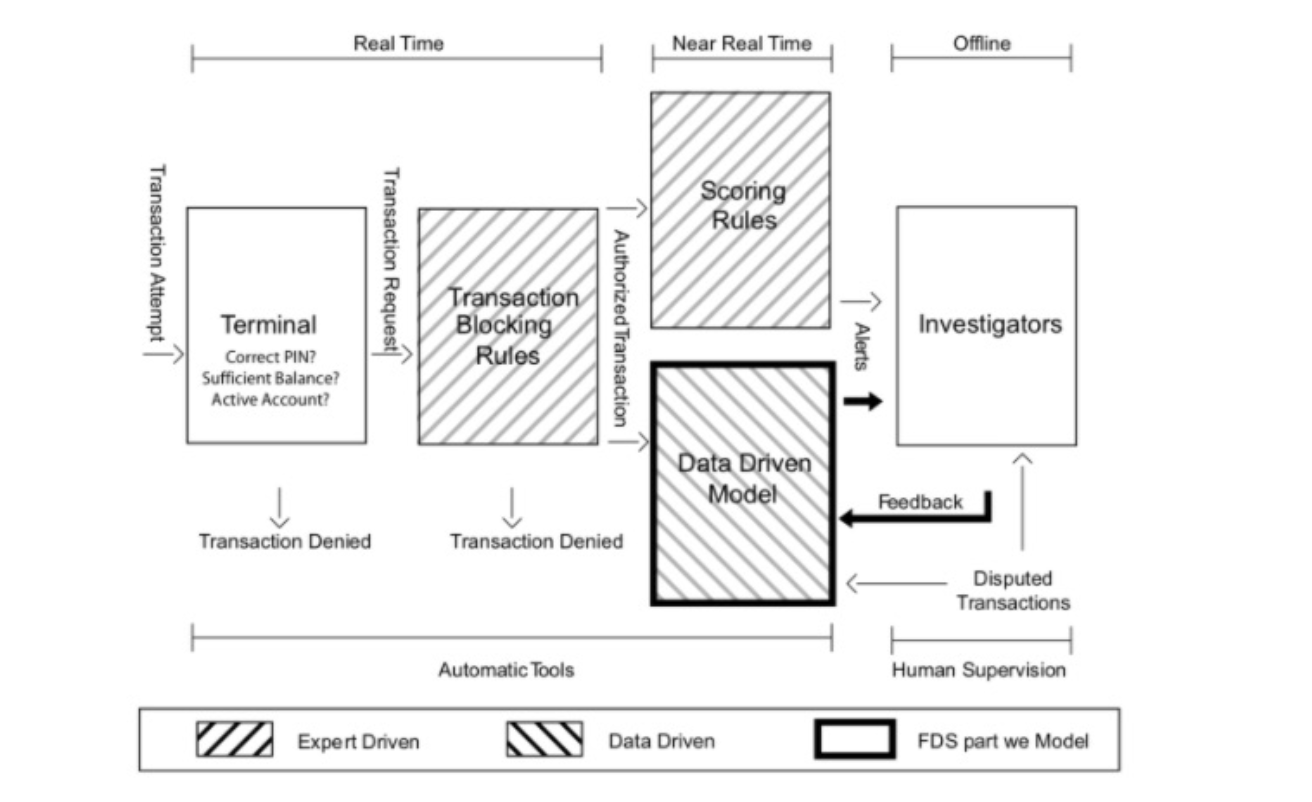
Fraud Detection System (@LeBorgne2022)

Figure 5.1: Fraud Detection System (Le Borgne et al. (2022))

Next we will discuss a brief example on using ML for Fraud Detection using Labelled data

16.2 Detecting Fraud in Transaction Data

16.2.1 Data

  • The data is a sample from the simulated transaction dataset availabe on Kaggle.

  • The kaggle datasets link provides a description of the dataset.

  • The kaggle dataset is highly unbalanced and requires subsampling techniques like SMOTE.

  • Chapter-11 of the caret package manual provides a good introduction to subsampling for class imbalances.

  • The data sample here consists of 10000 observations of 80:20, fraud and no fraud classifications.

Overview of the data

data1 = readRDS("data/fraud_sim.rds")
head(data1)
        step     type    amount    nameOrig oldbalanceOrg newbalanceOrig
3193213  247 CASH_OUT  802421.4  C369107118      802421.4              0
6001559  427 TRANSFER  225324.0 C1109518048      225324.0              0
6009616  441 TRANSFER  107363.5  C564631760      107363.5              0
6020272  461 CASH_OUT 1028284.8 C2004363483     1028284.8              0
6034233  476 CASH_OUT 1146381.4  C169415375     1146381.4              0
1030588   74 TRANSFER 4582074.5 C1151172465     4582074.5              0
           nameDest oldbalanceDest newbalanceDest isFraud isFlaggedFraud
3193213  C463164064     11846261.7       12648683       1              0
6001559 C1691016675            0.0              0       1              0
6009616   C43570912            0.0              0       1              0
6020272  C165602524            0.0        1028285       1              0
6034233 C1774696541       484779.2        1631161       1              0
1030588 C2088124795            0.0              0       1              0
  • Data description
    • The data consists of 11 attributes
    • step: Unit of time, 1 step is 1 hour
    • Type: CASH-IN, CASH-OUT, DEBIT, PAYMENT and TRANSFER
    • amount: amount of the transaction in local currency
    • nameOrg: customer starting the transaction
    • oldbalanceorg: initial balance before the transaction
    • newlabalanceorig: balance after the transaction
    • nameDest: recepient ID of the transaction
    • oldBalanceDest: initial recepient balance before the transaction
    • newBalanceDest: recepients balance after the transaction
    • isFraud: is fradualant (1), not fradualant (0)
    • isFlaggedFraud: flags illegal attemps to transfer more that 200,000 units at a time

16.2.2 Summary of the data

library(dplyr)
library(psych)
library(pastecs)
library(tidyr)
library(pander)
pander(stat.desc(data1))
Table continues below
  step type amount nameOrig oldbalanceOrg
nbr.val 10000 NA 10000 NA 10000
nbr.null 0 NA 3 NA 2683
nbr.na 0 NA 0 NA 0
min 1 NA 0 NA 0
max 743 NA 22925830 NA 59585040
range 742 NA 22925830 NA 59585040
sum 2671835 NA 4.433e+09 NA 9.918e+09
median 255.5 NA 108649 NA 31011
mean 267.2 NA 443257 NA 991799
SE.mean 1.67 NA 13125 NA 30621
CI.mean.0.95 3.273 NA 25728 NA 60022
var 27878 NA 1.723e+12 NA 9.376e+12
std.dev 167 NA 1312501 NA 3062058
coef.var 0.6249 NA 2.961 NA 3.087
Table continues below
  newbalanceOrig nameDest oldbalanceDest newbalanceDest
nbr.val 10000 NA 10000 10000
nbr.null 6619 NA 4709 4038
nbr.na 0 NA 0 0
min 0 NA 0 0
max 49585040 NA 93819985 94779646
range 49585040 NA 93819985 94779646
sum 7.137e+09 NA 9.446e+09 1.202e+10
median 0 NA 42762 195569
mean 713720 NA 944604 1202204
SE.mean 27920 NA 28396 32128
CI.mean.0.95 54729 NA 55661 62978
var 7.795e+12 NA 8.063e+12 1.032e+13
std.dev 2791998 NA 2839565 3212822
coef.var 3.912 NA 3.006 2.672
  isFraud isFlaggedFraud
nbr.val 10000 10000
nbr.null 8000 9996
nbr.na 0 0
min 0 0
max 1 1
range 1 1
sum 2000 4
median 0 0
mean 0.2 4e-04
SE.mean 0.004 2e-04
CI.mean.0.95 0.007841 0.000392
var 0.16 0.0003999
std.dev 0.4 0.02
coef.var 2 49.99 
# summarise(data1) %>% select(name,type,na, mean, median, min, max, nlevs)
# summary(data1)
  • Number of frauds/nofrauds
prop.table(table(data1$isFraud))

  0   1 
0.8 0.2

16.2.3 Visualisation

library(ggplot2)
theme_set(theme_minimal())  #globally sets the theme
data1 %>%
    ggplot(aes(isFraud, fill = factor(isFraud))) + geom_bar(stat = "count") + labs(x = "Fraud vs Not Fraud",
    y = "Frequency", fill = "FraudVNon-Fraud")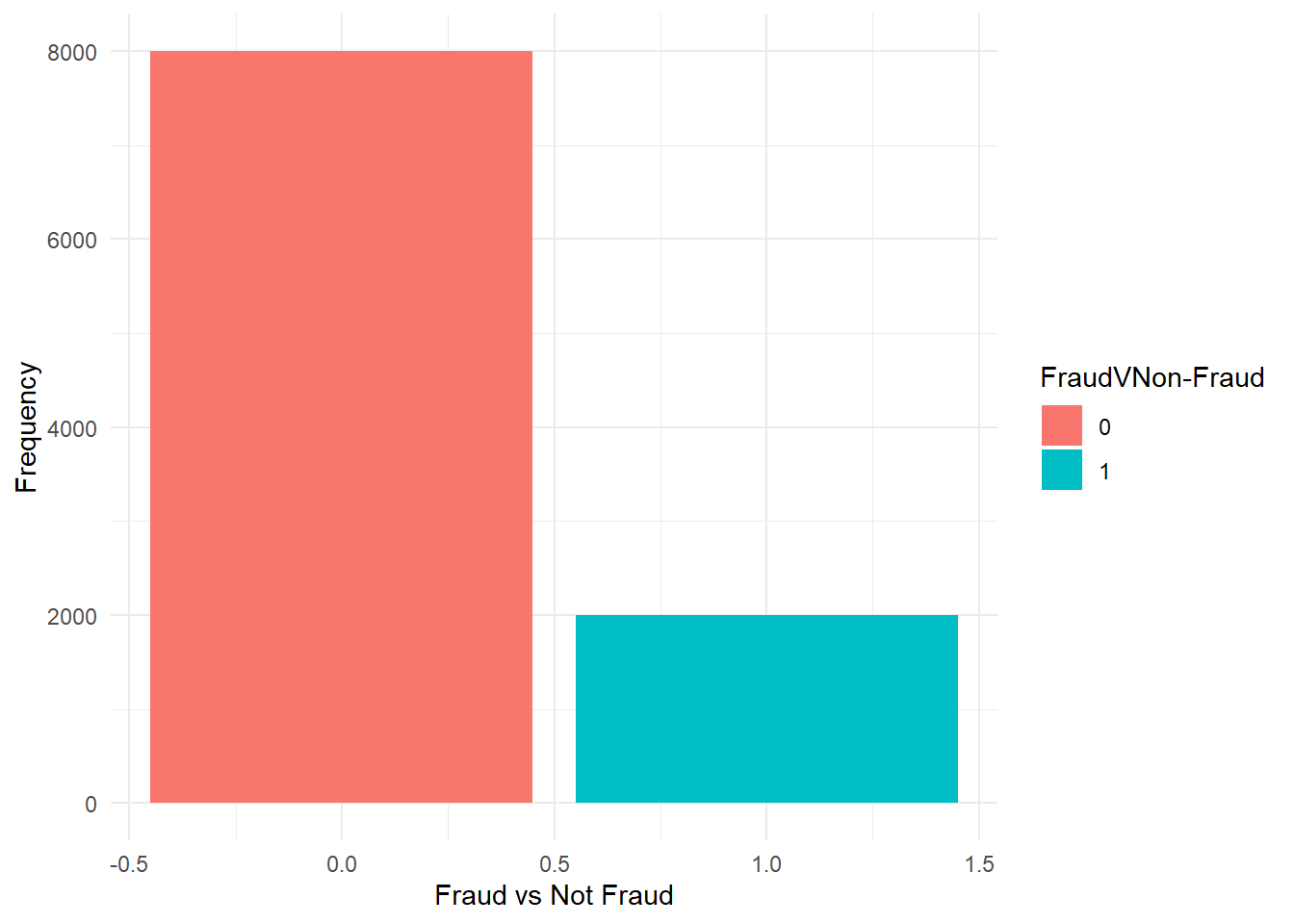
FraudVNon-Fraud

Figure 16.1: FraudVNon-Fraud

  • Transactions based on Fraud
data1 %>%
    ggplot(aes(x = type, fill = factor(isFraud))) + geom_bar()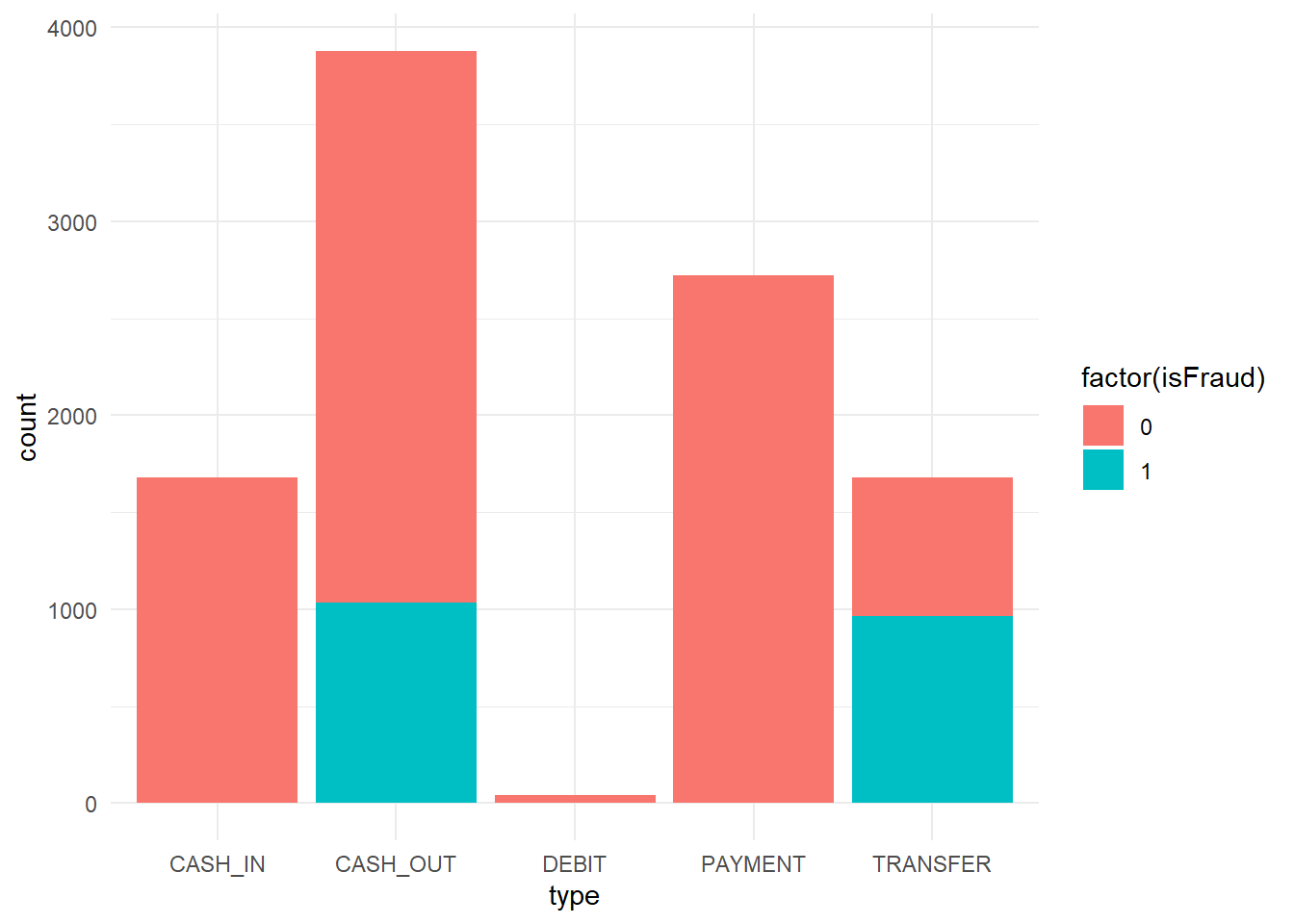
Transaction by Fraud

Figure 16.2: Transaction by Fraud

The figure shows that most frauds in the data sample are committed in CASH_OUT of in TRANSFER transaction type

  • Distribution of Transactions
library(dplyr)
library(scales)
data1 %>%
    filter(isFraud == 1) %>%
    ggplot(aes(amount)) + geom_histogram() + scale_x_continuous(labels = comma)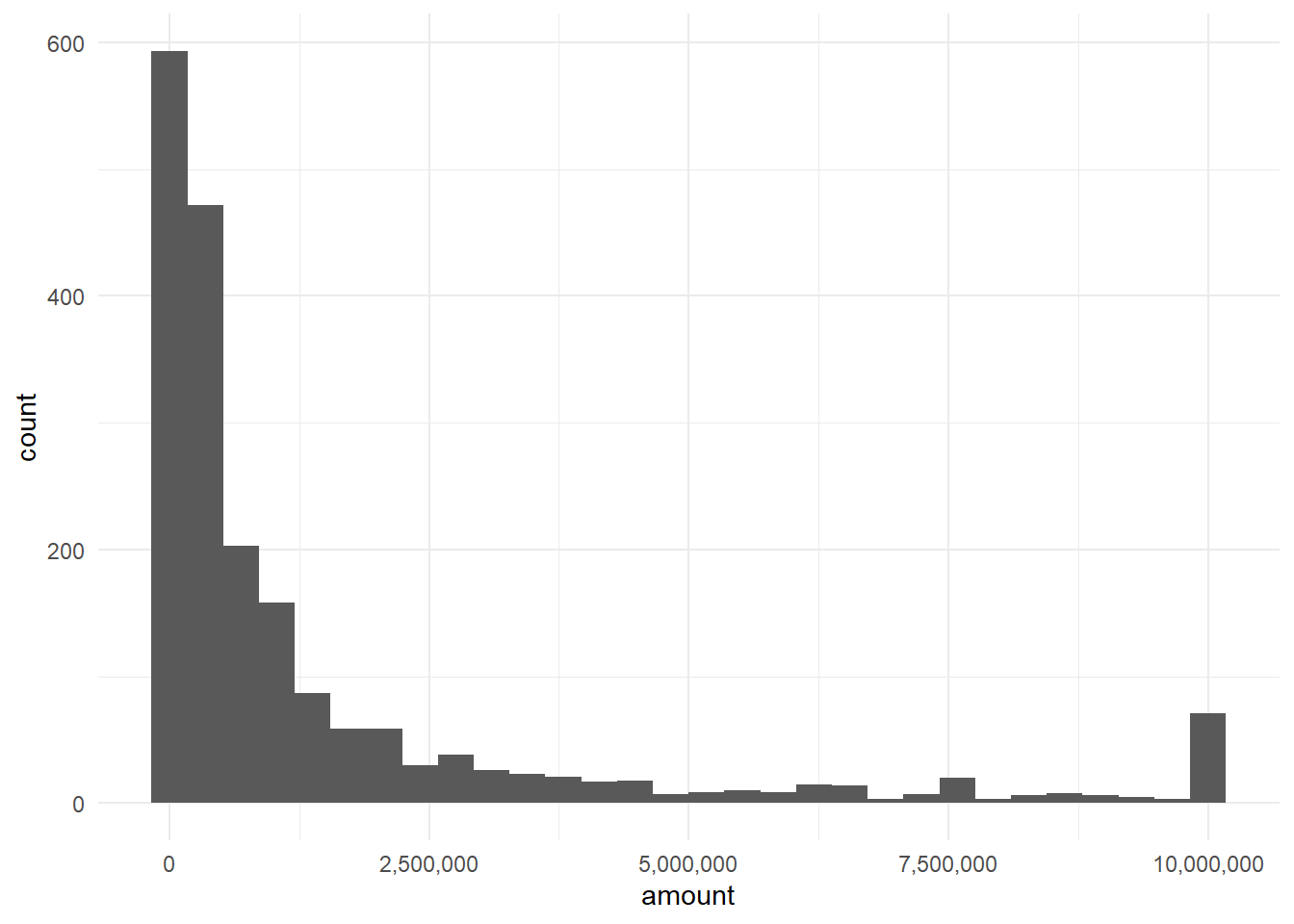
Fradualent Amount

Figure 16.3: Fradualent Amount

  • What about balance in accounts?
p1 = data1 %>%
    ggplot(aes(x = factor(isFraud), y = log(oldbalanceOrg), fill = factor(isFraud))) +
    geom_boxplot() + labs(title = "old balance in sender account")
p2 = data1 %>%
    ggplot(aes(x = factor(isFraud), y = log(oldbalanceDest), fill = factor(isFraud))) +
    geom_boxplot() + labs(title = "old balance in receiver account")
library(gridExtra)
grid.arrange(p1, p2, nrow = 1)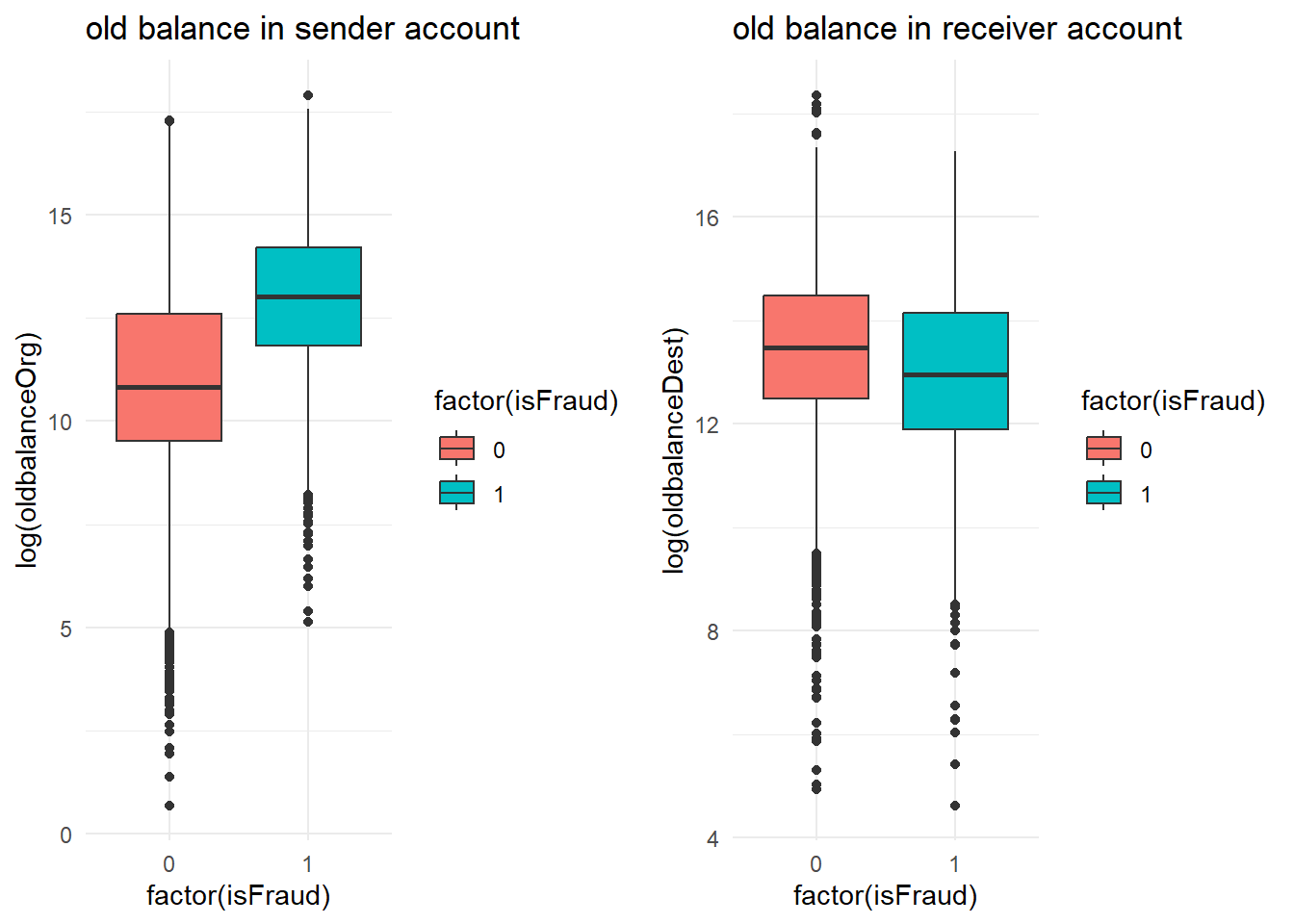
Balance (sender/receiver)

Figure 16.4: Balance (sender/receiver)

Task: Create other visualisations to visually analyse the data

16.3 ML Model

  • There are various ML models possible but we will use KNN, Random Forests and Neural Networks

16.3.1 Setup

Select the most useful columns

library(fastDummies)  #for creating dummy columns
data2 = data1 %>%
    select(-c("step", "nameOrig", "nameDest", "isFlaggedFraud")) %>%
    filter(type %in% c("CASH_OUT", "TRANSFER"))
data3 = dummy_cols(data2)  #takes the column with factors and creates dummies based on that
data3$isFraud = as.factor(data3$isFraud)
data3 = data3[, -1]

16.3.2 Sampling and Resampling

  • As this is a sample which does not depend on the time series structure, we can use random sampling stratified by the default
library(rsample)
set.seed(123)
idx = initial_split(data3, prop = 0.7, strata = "isFraud")
d_train1 = training(idx)
d_test1 = testing(idx)
  • Resampling
library(caret)

cntrl1 = trainControl(method = "repeatedcv", number = 10, repeats = 2, allowParallel = TRUE)
prep1 = c("center", "scale", "zv")

16.3.3 KNN

set.seed(123)
mod1_fraud_knn = train(isFraud ~ ., data = d_train1, method = "knn", tuneLength = 10,
    preProcess = prep1, trControl = cntrl1)
  • Model
mod1_fraud_knn
k-Nearest Neighbors 

3889 samples
   7 predictor
   2 classes: '0', '1' 

Pre-processing: centered (7), scaled (7) 
Resampling: Cross-Validated (10 fold, repeated 2 times) 
Summary of sample sizes: 3500, 3500, 3500, 3500, 3500, 3500, ... 
Resampling results across tuning parameters:

  k   Accuracy   Kappa    
   5  0.9497300  0.8905007
   7  0.9483165  0.8873509
   9  0.9466455  0.8834357
  11  0.9458736  0.8816692
  13  0.9429167  0.8750019
  15  0.9411165  0.8707704
  17  0.9381596  0.8640186
  19  0.9368746  0.8611598
  21  0.9343039  0.8554145
  23  0.9328887  0.8522490

Accuracy was used to select the optimal model using the largest value.
The final value used for the model was k = 5.
  • Predictive Accuracy
set.seed(123)
pred1 = predict(mod1_fraud_knn, newdata = d_test1)
confusionMatrix(pred1, d_test1$isFraud)
Confusion Matrix and Statistics

          Reference
Prediction    0    1
         0 1026   50
         1   41  550
                                          
               Accuracy : 0.9454          
                 95% CI : (0.9334, 0.9558)
    No Information Rate : 0.6401          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.8811          
                                          
 Mcnemar's Test P-Value : 0.4017          
                                          
            Sensitivity : 0.9616          
            Specificity : 0.9167          
         Pos Pred Value : 0.9535          
         Neg Pred Value : 0.9306          
             Prevalence : 0.6401          
         Detection Rate : 0.6155          
   Detection Prevalence : 0.6455          
      Balanced Accuracy : 0.9391          
                                          
       'Positive' Class : 0

16.3.4 Random Forests

mtry = sqrt(ncol(d_test1))
tunegrid = expand.grid(.mtry = mtry)
library(doParallel)
cl = makePSOCKcluster(detectCores()/2)
registerDoParallel(cl)
set.seed(123)


rf_fraud = train(isFraud ~ ., data = d_train1, method = "rf", tuneGrid = tunegrid,
    trControl = cntrl1, preProcess = prep1)
stopCluster(cl)
registerDoSEQ()
  • Model
rf_fraud
Random Forest 

3889 samples
   7 predictor
   2 classes: '0', '1' 

Pre-processing: centered (7), scaled (7) 
Resampling: Cross-Validated (10 fold, repeated 2 times) 
Summary of sample sizes: 3500, 3500, 3500, 3500, 3500, 3500, ... 
Resampling results:

  Accuracy   Kappa    
  0.9755708  0.9469659

Tuning parameter 'mtry' was held constant at a value of 2.828427
  • Predictive Accuracy
set.seed(123)
pred2 = predict(rf_fraud, newdata = d_test1)
confusionMatrix(pred2, d_test1$isFraud)
Confusion Matrix and Statistics

          Reference
Prediction    0    1
         0 1049   15
         1   18  585
                                          
               Accuracy : 0.9802          
                 95% CI : (0.9723, 0.9863)
    No Information Rate : 0.6401          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.9571          
                                          
 Mcnemar's Test P-Value : 0.7277          
                                          
            Sensitivity : 0.9831          
            Specificity : 0.9750          
         Pos Pred Value : 0.9859          
         Neg Pred Value : 0.9701          
             Prevalence : 0.6401          
         Detection Rate : 0.6293          
   Detection Prevalence : 0.6383          
      Balanced Accuracy : 0.9791          
                                          
       'Positive' Class : 0

16.3.5 NNET

library(doParallel)
cl = makePSOCKcluster(detectCores()/2)
registerDoParallel(cl)
set.seed(123)


nnet_fraud = train(isFraud ~ ., data = d_train1, method = "nnet", trControl = cntrl1,
    preProcess = prep1)
# weights:  28
initial  value 2899.085170 
iter  10 value 1454.628563
iter  20 value 537.562073
iter  30 value 332.100069
iter  40 value 189.749918
iter  50 value 152.552874
iter  60 value 112.587854
iter  70 value 106.284558
iter  80 value 98.840062
iter  90 value 95.032644
iter 100 value 93.058743
final  value 93.058743 
stopped after 100 iterations
stopCluster(cl)
registerDoSEQ()
  • Model
nnet_fraud
Neural Network 

3889 samples
   7 predictor
   2 classes: '0', '1' 

Pre-processing: centered (7), scaled (7) 
Resampling: Cross-Validated (10 fold, repeated 2 times) 
Summary of sample sizes: 3500, 3500, 3500, 3500, 3500, 3500, ... 
Resampling results across tuning parameters:

  size  decay  Accuracy   Kappa    
  1     0e+00  0.9805866  0.9575230
  1     1e-04  0.9820012  0.9610373
  1     1e-01  0.9553895  0.9021244
  3     0e+00  0.9845725  0.9665263
  3     1e-04  0.9822559  0.9615537
  3     1e-01  0.9628459  0.9186841
  5     0e+00  0.9832875  0.9636761
  5     1e-04  0.9823854  0.9618194
  5     1e-01  0.9633603  0.9197440

Accuracy was used to select the optimal model using the largest value.
The final values used for the model were size = 3 and decay = 0.
  • Predictive Accuracy
set.seed(123)
pred3 = predict(nnet_fraud, newdata = d_test1)
confusionMatrix(pred3, d_test1$isFraud)
Confusion Matrix and Statistics

          Reference
Prediction    0    1
         0 1060    9
         1    7  591
                                          
               Accuracy : 0.9904          
                 95% CI : (0.9845, 0.9945)
    No Information Rate : 0.6401          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.9792          
                                          
 Mcnemar's Test P-Value : 0.8026          
                                          
            Sensitivity : 0.9934          
            Specificity : 0.9850          
         Pos Pred Value : 0.9916          
         Neg Pred Value : 0.9883          
             Prevalence : 0.6401          
         Detection Rate : 0.6359          
   Detection Prevalence : 0.6413          
      Balanced Accuracy : 0.9892          
                                          
       'Positive' Class : 0

References

Al-Hashedi, K. G., & Magalingam, P. (2021). Financial fraud detection applying data mining techniques: A comprehensive review from 2009 to 2019. Computer Science Review, 40, 100402. https://doi.org/https://doi.org/10.1016/j.cosrev.2021.100402
Ali, A., Abd Razak, S., Othman, S. H., Eisa, T. A. E., Al-Dhaqm, A., Nasser, M., … Saif, A. (2022). Financial fraud detection based on machine learning: A systematic literature review. Applied Sciences, 12(19). https://doi.org/10.3390/app12199637
Ashtiani, M. N., & Raahemi, B. (2021). Intelligent fraud detection in financial statements using machine learning and data mining: A systematic literature review. IEEE Access, 10, 72504–72525.
Bin Sulaiman, R., Schetinin, V., & Sant, P. (2022). Review of machine learning approach on credit card fraud detection. Human-Centric Intelligent Systems, 1–14.
Le Borgne, Y.-A., Siblini, W., Lebichot, B., & Bontempi, G. (2022). Reproducible machine learning for credit card fraud detection - practical handbook. Université Libre de Bruxelles. Retrieved from https://fraud-detection-handbook.github.io/fraud-detection-handbook/Foreword.html
Sadgali, I., Sael, N., & Benabbou, F. (2019). Performance of machine learning techniques in the detection of financial frauds. Procedia Computer Science, 148, 45–54.